রাদারফোর্ড মডেলের ত্রুটি দুর করার জন্য প্রথম সফল পদক্ষেপ নিয়েছিলেন ডেনমার্কের বিজ্ঞানী নিল্স বোর। তিনি ১৯১৩ সালে পরমাণুর গঠন সম্পর্কে কিছু নতুন প্রস্তাবনা করেন যা বোরের মডেল নামে পরিচিত। বোরের মডেল কতগুলি প্রতিপাদ্যের উপর প্রতিষ্ঠিতঃ
১. পরমাণুর মধ্যে ইলেকট্রনগুলি নিউক্লিয়াসকে প্রদক্ষিণ করে.
২. ইলেকট্রনগুলি নিউক্লিয়াসকে বেষ্টন করে শুধুমাত্র কিছু নির্দিষ্ট কক্ষপথেই ঘুরতে পারে। ওই কক্ষপথগুলিতে প্রদক্ষিণ করার সময় ইলেকট্রন কোন রকম শক্তি বিকিরণ করেনা (যদিও ওদের গতির ত্বরণ বিদ্যমান)। নিউক্লিয়াস থেকে ওই কক্ষপথগুলির দূরত্ব ও কক্ষপথে আবর্তনকারী ইলেকট্রনের শক্তির শুধু নির্দিষ্ট কিছু মান থাকতে পারে (discrete values)। এই রকম কক্ষপথগুলিকে ষ্টেশনারী অরবিট বা স্থানু কক্ষপথ বলা হয়। যদি একটি নির্দিষ্ট স্থানু কক্ষপথের ব্যাসার্ধ r হয় ও ওই কক্ষপথে আবর্তনকারী ইলেকট্রনের গতিবেগ v হয়, তাহলে ষ্টেশনারী অরবিট গুলির জন্য এই শর্তটি প্রযোজ্যঃ , এখানে
কেজি হল ইলেক্ট্রনের ভর ও
জুল-সেকেন্ড হল প্লাঙ্ক কনষ্টান্ট।
।
একটি ধনাত্মক পূর্ণসংখ্যা, যার মান ১ থেকে শুরু হয় (১, ২, ৩, ৪, …….ইত্যাদি)। এই শর্তটিকে বোরের কোয়ান্টাইজেশন নীতি (Bohr’s quantisation principle ) বলা হয়।
৩. শুধুমাত্র একটি স্থানু কক্ষপথ থেকে অন্য একটি স্থানু কক্ষপথে স্থানান্তরণের মাধ্যমেই ইলেকট্রনগুলি শক্তি লাভ করতে বা হারাতে পারে। কম ব্যাসার্ধের (কম শক্তির) কক্ষপথ থেকে বেশী ব্যাসার্ধের (বেশী শক্তির) কক্ষপথে গেলে ইলেকট্রন বাইরে থেকে তড়িৎ-চুম্বকীয় শক্তি শোষণ করে। আর যদি উল্টোটা হয়, অর্থাৎ বেশী থেকে কম ব্যাসার্ধের কক্ষপথে গেলে ইলেকট্রন থেকে তড়িৎ-চুম্বকীয় তরঙ্গ রূপে শক্তি বিকিরীত হয়। যদি ইলেকট্রনের স্থানান্তরণে জরিত কক্ষপথ দুটির শক্তি ও
হয়, তবে শোষিত বা বিকিরীত তড়িৎ-চুম্বকীয় তরঙ্গের কম্পাঙ্ক (
) এই সমীকরণটি মেনে চলেঃ
(1)
যেখানে । এর থেকে এটাও বোঝা যায় যে পরমাণু থেকে যে আলোক বা তড়িৎ-চুম্বকীয় তরঙ্গ বের হয় তার বর্ণালী নিরবিচ্ছিন্ন (conti\nuous spectrum) হবেনা। যেহেতু,
ও
-র শুধু কতগুলি নির্দিষ্ট মান থাকতে পারে, তাই পরমাণু থেকে নির্গত আলোর কম্পাঙ্কেরও (
) শুধু কতগুলি নির্দিষ্ট বিযূক্ত মান (discreet values) সম্ভব। বিজ্ঞানের পরিভাষায়, পরমাণু থেকে রেখা বর্ণালী (line spectrum) যুক্ত আলো বিকিরীত হয়। একই কারণে পরমাণু শুধু কিছু নির্দিষ্ট কম্পাঙ্কের বা রঙের আলো শোষণ করতে পারে।
উপরোক্ত মডেল যে শুধু পরমাণুর স্থায়ীত্ব সুনিশ্চিত করে তাই নয়, পারমাণবিক বর্ণালীরও উপযুক্ত ব্যাখ্যা প্রদান করে। কিন্তু তোমরা হয়তো এতক্ষণে বুঝতে পেরেছো যে বোরের মডেলে একটা গুরুতর গোলমাল আছে! ইলেকট্রনগুলি’তো নিউক্লিয়াসকে কেন্দ্র করে ঘুরছে, তার মানে নিশ্চয়ই ওদের ত্বরণ আছে। তথাপি ওরা শক্তি বিকিরণ করে নিউক্লিয়াসের মধ্যে গিয়ে পড়ছে না কেন? কেনই বা স্থানু কক্ষপথের (stationary orbit) ক্ষেত্রে -এই শর্তটি প্রযোজ্য? বোর এসবের কোন ব্যাখ্যা দেননি। বোরের মডেলের এই গন্ডগোল দূর করেছিলেন এক ফরাসী বিজ্ঞানী। এর পরের পোষ্টে আমরা সেটাই দেখবো! তদবধি ভালো থেকো ও পড়তে থাকো।
বোর কিভাবে সিদ্ধান্তে আসলেন যে ইলেকট্রনের কৌনিক ভরবেগ nh/2pi এর পূর্ণ গুনেতিক হবে? আমি আমার ক্লাস টিচারকে একদিন এই বিষটা জিজ্ঞেস করেছিলাম। তিনি বলতে পারেননি। দয়া করে জানাবেন। এটা দীর্ঘ দিনের কৈতুহল।
বোর তার মডেল আবিষ্কারের আগে পরমানুর একমাত্র মডেল ছিল রাদারফোর্ডের সৌরজাগতিক মডেল। কিন্তু রাদারফোর্ড বুঝতে পেরেছিলেন যে ওই মডেল পুরোপুরি ঠিক নয়। তাই বোর যখন রাদারফোর্ডের ল্যাবরেটরিতে কাজ করতে গেলেন তখন রাদারফোর্ড বোর কে কাজ দিয়েছিলেন তার পরমানু সংক্রান্ত মডেলটির সমস্যা দূর করার। বোর এইভাবে এগিয়েছিলেন। উনি ক্লাসিক্যাল মেকানিক্স থেকে শুরু করেন। মনে কর ইলেকট্রনের কক্ষপথে একবার আবর্তন করতে সময় লাগে T। তাহলে ক্লাসিক্যাল মেকানিক্স অনুসারে ওই কক্ষপথে আবর্তনের ফলে যে কম্পাঙ্কের আলো নির্গত হবে তার কম্পাঙ্কও হবে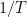 এর সমানুপাতিক। অর্থাৎ ওই আলোর ফোটনের শক্তি
এর সমানুপাতিক। অর্থাৎ ওই আলোর ফোটনের শক্তি  । এখন কেপলারের সূত্র থেকে জানা যায় যে কোন কক্ষপথের ক্ষেত্রে
। এখন কেপলারের সূত্র থেকে জানা যায় যে কোন কক্ষপথের ক্ষেত্রে  । অর্থাৎ
। অর্থাৎ  । আবার বৃত্তাকার কক্ষপথের জন্য ক্লাসিক্যাল মেকানিক্স থেকে,
। আবার বৃত্তাকার কক্ষপথের জন্য ক্লাসিক্যাল মেকানিক্স থেকে,
 , এবং
, এবং 
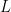 হল কৌনিক ভরবেগ,
হল কৌনিক ভরবেগ,  হল কক্ষপথের ব্যাসার্ধ,
হল কক্ষপথের ব্যাসার্ধ,  হল রৈখিক গতিবেগ। তাহলে উপরের দুটি সমীকরণ থেকে দেখা যাচ্ছে যে
হল রৈখিক গতিবেগ। তাহলে উপরের দুটি সমীকরণ থেকে দেখা যাচ্ছে যে  , এবং
, এবং  ।
।
যেখানে
অতএব, ……..(1)
……..(1) ….(2)
….(2)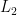 এবং
এবং  হয় তবে (2) নং সমীকরণ ব্যবহার করে,
হয় তবে (2) নং সমীকরণ ব্যবহার করে,
আবার কক্ষপথে ইলেকট্রনের মোট শক্তি
এবারে যদি মনে করা হয় যে এক কক্ষপথ থেকে পরের কক্ষপথে ইলেকট্রনের পতনের ফলেই ফোটন নির্গত হয় এবং ওই দুটি কক্ষপথের কৌনিক ভরবেগ যথাক্রমে
মনে কর যে পরপর অবস্থিত দুটি কক্ষপথের মাঝে কৌনিক ভরবেগের পার্থক্য , অর্থাৎ,
, অর্থাৎ,  , তবে,
, তবে,


যদি মনে করা হয় যে একটি খুব ক্ষুদ্র রাশি তবে,
একটি খুব ক্ষুদ্র রাশি তবে,
(1) ও (3) নং সমীকরণ তুলনা করে দেখা যায় যে, । অতএব যেকোনো দুটি পরপর অবস্থিত কক্ষপথের মাঝে কৌনিক ভরবেগের পার্থক্য
। অতএব যেকোনো দুটি পরপর অবস্থিত কক্ষপথের মাঝে কৌনিক ভরবেগের পার্থক্য  হবে। তার মনে হল
হবে। তার মনে হল  । এইভাবেই বোর তার মডেল বের করেছিলেন।
। এইভাবেই বোর তার মডেল বের করেছিলেন।
একটা বিষয় ঠিক বুঝতে পারিনি। বোর ফোটনের শক্তি dE কে কেন h/(2pi*T) এর সমানুপাতিক বিবেচনা করল। যেহেতু 2pi ধ্রুব সংখ্যা তাই ফোটনের শক্তিকে h/T এর সমানুপাতিকও বিবেচনা করা যায়। এক্ষেত্রে 2pi এর বিশেষত্ব কি?