আমরা এর আগের পোস্টে গতিবেগ ও ত্বরণের ফোর ভেক্টর সম্মন্ধে আলোচনা করেছি। আজকের বিষয়বস্তু হল ভরবেগের ফোর ভেক্টর, নিউটনের গতিসূত্র এবং ভর ও শক্তির তুল্যতা সম্মন্ধীয় আইনস্টাইনের সেই বিখ্যাত সমীকরণ। – এইটি বোধহয় পৃথিবীর সব থেকে বিখ্যাত সমীকরণ যা বিজ্ঞানী, তথাকথিত বিজ্ঞানী, মায় অবৈজ্ঞানীক, এমনকি ব্যবসাদারেরা পর্যন্ত মাথায় রাখে। এই তো সেদিন দেখতে পেলাম একটি রেস্তোরার নাম
। ভাবা যায়? কোনদিন আবার হয়তো দেখব যে শক্তিবর্দ্ধক ট্যাবলেটের নাম
! যাই হোক আমরা আমাদের আলোচ্য বিষয়ের দিকে দৃষ্টি ঘোরাই এবার, নাহলে ভাট বকে বকেই রাত কেটে যাবে। ধরা যাক কোন একটি বস্তু
ইনার্শিয়াল ফ্রেমের সাপেক্ষে কোন মুহূর্ত
তে
বেগে গতিশীল। তবে তোমরা দেখেছো যে ওর গতিবেগের ফোর ভেক্টর,
………… (1)
হল বস্তুর প্রপার টাইম। আমরা সরল করে দেখিয়েছি যে
, যেখানে
।
হল গতিবেগের ফোর ভেক্টরের স্থান সম্মন্ধীয় উপাদানগুলি দিয়ে তৈরি ত্রিমাত্রিক ভেক্টর। যদি বস্তুটির ভর
হয় তবে সাধারণ ভরবেগের মতই ভরবেগের ফোর ভেক্টরের সংজ্ঞা হল,
………… (2)
যেখানে হল ভরবেগের ফোর ভেক্টরের স্থানের মত (space like) উপাদানগুলি দিয়ে তৈরি ত্রিমাত্রিক ভেক্টর যা মূলত রিলেটিভিটিতে বস্তুর প্রকৃত ভরবেগ বা রিলেটিভিস্টিক ভরবেগ (relativistic momentum)। এখানে বলে রাখি যে কোন ফোর ভেক্টরের শূন্যতম উপাদানকে বলা হয় ওর সময়ের মত বা টাইমলাইক উপাদান এবং বাকি তিনটে উপাদানদের বলা হয় স্থানের মত বা স্পেসলাইক উপাদান। ভরবেগের ফোর ভেক্টরের সময়ের মত (time like) বা শূন্যতম উপাদান
আসলে কি সেটা বুঝতে গেলে আমাদের নিউটনের দ্বিতীয় গতিসূত্রের আপেক্ষিকতার সাথে সামঞ্জস্যপূর্ণরূপ (relativistic form of Newton’s second law) দেখতে হবে। সাধারণ নিউটনের সূত্রের মতই ভরবেগের ফোর ভেক্টরের পরিবর্তনের হার প্রযুক্ত বলের ফোর ভেক্টরের
সমান। তবে এখানে ভরবেগের পরিবর্তনের হার হিসেব করা হয় বস্তুর প্রপার টাইমের সাপেক্ষে। অর্থাৎ,
…………………… (3)
যদি বলের ফোর ভেক্টরের স্থানের মত (spacelike) উপাদানগুলিকে একত্র করে তৈরি ত্রিমাত্রিক ভেক্টরকে দিয়ে লেখা হয় তাহলে,
………… (4)
যেখানে সাধারণ নিউটনিয় বলবিদ্যার মতই ; তবে এখানে
কিন্তু রিলেটিভিস্টিক বা রিলেটিভিটির সাথে সামঞ্জস্যপূর্ণ ভরবেগ
এবং
কে বলা হয় রিলেটিভিস্টিক বল (এটা ফোর ভেক্টর নয়)। এবারে এর আগের পোস্টে আমরা দেখেছি যে ফোর ভেলোসিটি
ও ফোর ত্বরণ
পরষ্পরের সাথে অর্থোগোনাল, বা,
…………….. (5)
যেখানে হল মেট্রিক টেন্সরের উপাদান।আবার যেহেতু
, অথবা
…….. (6)
অতএব,
……………. (7)
বা,
বা,
বা,
বা,
বা, ……………… (8)
এখন তোমরা জানো যে বল ও গতিবেগের স্কেলার গুণফল হল বস্তুর কাজ করার হার বা ওর ক্ষমতা। অর্থাৎ , যেখানে
হল কোন মুহূর্ত
তে বস্তুটির শক্তি। অতএব,
…………. (9)
আবার (3) নং সমীকরণ ব্যবহার করে, , তাই, (9) নম্বর সমীকরণ থেকে,
………… (10)
অতএব ভরবেগের ফোর ভেক্টরের সময়ের মত বা শূন্যতম উপাদান বস্তুর শক্তি প্রকাশ করে। সুতরাং আমরা লিখতে পারি, । এর আগের পোস্টে তোমরা দেখেছো যে,
বা,
বা,
বা,
বা,
বা,
বা, ………………. (11)
এটাই বিশেষ আপেক্ষিকতায় কোন কণার মোট শক্তির সমীকরণ। লক্ষ্য কর যে যদি বস্তুটি কোন ফ্রেমের সাপেক্ষে স্থির থাকে তবে ওর ভরবেগ
, অতএব,
………………….. (12)
সুতরাং বস্তুটি স্থির থাকলেও ওর মধ্যে পরিমান শক্তি থেকেই যায় যা ওই বস্তুর ভরের উপর নির্ভর করে। এই শক্তিকে বলা হয় বস্তুর স্থিরাবস্থার শক্তি বা রেস্ট এনার্জি (rest energy)। এই রেস্ট এনার্জি মূলত কণার ভরের জন্য ওর শক্তিকেই বোঝায়। এর থেকে বোঝা যায় যে ভর ও শক্তি মূলত একই সত্ত্বার ভিন্ন প্রকাশ মাত্র, একটি অন্যটিতে পরিবর্তিত হতে পারে। সত্যি কথা বলতে গেলে তেজস্ক্রিয় পরমানুর কেন্দ্রে হামেশাই পদার্থ শক্তিতে ও শক্তি পদার্থে পরিণত হয় এবং এটাও সর্বজনবিদিত যে আইনস্টাইনের এই বিখ্যাত সমীকরণ ব্যবহার করেই এটম বোমা ও হাইড্রোজেন বোমা তৈরি করা হয়েছে, যেখানে কিছুটা পরিমণ পদার্থ বিপুল পরিমান শক্তিতে মুহূর্তের মধ্যে রূপান্তরিত হয়ে বিস্ফোরণ ঘটায়। আর যেহেতু ভর শক্তিতে ও শক্তি ভরে রূপান্তরিত হতে পারে, তাই আলাদাভাবে ভর ও শক্তির সংরক্ষণের সমীকরণ অর্থহীন। তার বদলে বলা হয় যে কোন আবদ্ধ সিস্টেমের ভর ও শক্তির মোট পরিমান সংরক্ষিত থাকে। এই নীতিকে বলা হয় ভর-শক্তির সংরক্ষন নীতি। যেহেতু আলোর বেগ সেকেন্ডে প্রায়
km, তাই উপরোক্ত সমীকরণ থেকে এও দেখা যায় যে খুব স্বল্প পরিমান ভর থেকে বিপুল পরিমান শক্তি উৎপন্ন হতে পারে। এইজন্য শক্তিকে লঘীভূত ভর ও ভরকে ঘনীভূত শক্তি হিসেবে দেখা যেতে পারে। নিউক্লিয়ার রিয়েক্টর ব্যবহার করে ভর থেকে রূপান্তরিত শক্তিকে ব্যবহারের উপযোগী বিদ্যূৎ শক্তিতে পরিণত করা সম্ভব।
(2) ও (10) নম্বর সমীকরণ দুটোর থেকে দেখা যায় যে,
……….. (13)
যদি কোন ভরযুক্ত কণার বেগ কোন ইনার্শিয়াল ফ্রেমের সাপেক্ষে আলোর বেগের তুলনায় খুব কম হয় $latex (v<
Darun post.. Blog er pathok er sonkha bere6e dekhe khub valo lagche…
ধন্যবাদ Sujoy. পাঠক সংখ্যা কিছু বেড়েছে, আরও বাড়লে বেশি ভাল লাগবে। 😉
এখানে বলা হয়েছে “আধুনিক রীতি অনুসারে কোন বস্তুর ভর একটি স্কেলার রাশি, অর্থাৎ সমস্ত ইনার্শিয়াল ফ্রেমেই ওর মান একই থাকে ” — কিন্তু ভরের পরিবর্তনের যে প্রমান টা আমরা জানি , সেটা কি ভুল ? সেটার কোথায় ভুল ছিল ?
তুমি যে ডেরিভেশন জানো সেটার কোথাও ভুল ছিলনা। রিলেটিভিস্টিক ভর (যা গতিবেগের উপর নির্ভর করে) এবং ইনভ্যারিয়েন্ট ভর
(যা গতিবেগের উপর নির্ভর করে) এবং ইনভ্যারিয়েন্ট ভর 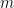 (যা প্রত্যেক ফ্রেমে একই থাকে) একই ঘটনাকে দুটি আলাদা রীতিতে প্রকাশ করার উপায় মাত্র। তোমার যেটা পছন্দ তুমি সেটা ব্যবহার করতে পার। যেমন
(যা প্রত্যেক ফ্রেমে একই থাকে) একই ঘটনাকে দুটি আলাদা রীতিতে প্রকাশ করার উপায় মাত্র। তোমার যেটা পছন্দ তুমি সেটা ব্যবহার করতে পার। যেমন  , এই সমীকরণকে তুমি লিখতে পার
, এই সমীকরণকে তুমি লিখতে পার  , যেখানে
, যেখানে  হল রিলেটিভিস্টিক ভর। একইভাবে
হল রিলেটিভিস্টিক ভর। একইভাবে  কে তুমি লিখতে পার
কে তুমি লিখতে পার  । তবে তুমি যে রীতিই ব্যবহার কর না কেন মূল ফিজিক্স তাতে পরিবর্তিত হয় না। অর্থাৎ রিলেটিভিস্টিক ভর বা ইনভ্যারিয়েন্ট ভর, এদের যেটাকেই তুমি ব্যবহার কর, বস্তুর শক্তি ও ভরবেগের মান দুক্ষেত্রেই একই বের হবে (শুধু তোমাকে মনে রাখতে হবে যে তুমি যেন উপযুক্ত সমীকরণ ব্যবহার কর।) সাধারণত রিলেটিভিটি নিয়ে যারা কাজকর্ম করেন তারা ইনভ্যারিয়েন্ট ভর ব্যবহারের পক্ষপাতী; অপরপক্ষে পর্টিকল ফিজিক্সের গবেষকদের পছন্দ রিলেটিভিস্টিক ভর।
। তবে তুমি যে রীতিই ব্যবহার কর না কেন মূল ফিজিক্স তাতে পরিবর্তিত হয় না। অর্থাৎ রিলেটিভিস্টিক ভর বা ইনভ্যারিয়েন্ট ভর, এদের যেটাকেই তুমি ব্যবহার কর, বস্তুর শক্তি ও ভরবেগের মান দুক্ষেত্রেই একই বের হবে (শুধু তোমাকে মনে রাখতে হবে যে তুমি যেন উপযুক্ত সমীকরণ ব্যবহার কর।) সাধারণত রিলেটিভিটি নিয়ে যারা কাজকর্ম করেন তারা ইনভ্যারিয়েন্ট ভর ব্যবহারের পক্ষপাতী; অপরপক্ষে পর্টিকল ফিজিক্সের গবেষকদের পছন্দ রিলেটিভিস্টিক ভর।
তাহলে আমরা রিলেটিভিস্টিক চার্জ বলে কোন জিনিশ আমদানি করতে পারি না ? সেক্ষেত্রে সমস্যাটা কোথায় ? আপনি নিশ্চয়ই বুঝতে পেরেছেন আমি কেন কথাটা বলছি ।
আমি বুঝতে পারছি তুমি কোন কথাটা বলতে চাইছো। 😉 গতশীল বস্তুর শক্তি ও ভরবেগ দুভাবে ব্যাখ্যা করা সম্ভব – ইনভ্যারিয়েন্ট ভর ও রিলেটিভিস্টিক ভর ব্যবহার করে। তুমি যদি এটা মনে কর যে বস্তুর ভর গতিবেগের উপর নির্ভর করেনা তবে তুমি এক রকম সমীকরণ ব্যবহার করেবে, আর যদি তুমি মনে কর যে ভর গতিবেগের উপর নির্ভরশীল তবে তুমি আরেক রকম সমীকরণ ব্যবহার করবে। কিন্তু দুক্ষেত্রেই মোট শক্তি ও ভরবেগের মান তুমি একই পাবে। অপরপক্ষে আগেই বলেছি যে বস্তুর আধান গতিবেগের উপর নির্ভর করেনা। এটা পরিক্ষীত সত্য। তাহলে কেন তুমি রিলেটিভিস্টিক চার্জের ধারণা আমদানি করবে? চার্জের মান তো সমস্ত ফ্রেমে একই থাকছে।