মিনকোভস্কি স্থানে গতিবেগ ও ত্বরণের ফোর ভেক্টর (Four velocity and accelaration)

সাধারণ ত্রিমাত্রিক ভেক্টর ব্যবহার করে লেখা নিউটনের গতিসূত্র লোরেন্‍ৎস রূপান্তরণ এবং বিশেষ আপেক্ষিকতার সাথে সামঞ্জস্যপূর্ণ নয়। এটা সহজেই বোঝা যায়। নিউটনে সূত্র অনুসারে কোন কণার উপর ক্রমাগত বল প্রয়োগ করতে থাকলে ওর গতিবেগ বাড়তে বাড়তে একসময় আলোর গতিবেগের থেকেও বেশি হয়ে যাবে, যা বিশেষ আপেক্ষিকতায় অসম্ভব। সেজন্যেই নিউটনের সূত্রকে বিশেষ আপেক্ষিকতার উপযোগী করে লেখা প্রয়োজন। ত্রিমাত্রিক ভেক্টর ব্যবহার করে লেখা নিউটনের সূত্র কেবল সেইসব ক্ষেত্রেই প্রযোজ্য যেখানে কণা বা কণাসমষ্টির গতিবেগ আলোর থেকে অনেক কম। লোরেন্‍ৎস রূপান্তরণের পরেও অপরিবর্তিত থাকতে হলে ও বিশেষ আপেক্ষিকতার সাথে সুসংগত হতে গেলে নিউটনের সূত্রকে ফোর ভেক্টরের মাধ্যমে লিখতে হবে। সেজন্য আমাদের প্রয়োজন চতুর্মাত্রিক গতিবেগ ও চতুর্মাত্রিক ত্বরণ যাদেরকে এরপর থেকে আমরা যথাক্রমে ফোরভেলোসিটি (four velocity) ও ফোর ত্বরণ (four accelaration) নামে ডাকবো। গতিবেগ ও ত্বরণের ফোর ভেক্টর নিয়ে অধিক আলোচনার পূর্বে একবার আমরা ফোর ভেক্টরের সংজ্ঞাটা একটু ঝালিয়ে নিচ্ছি। লোরেন্‍ৎস রূপান্তরণের ফলে যদি নির্দিষ্ট ক্রমে সাজানো চারটি সংখ্যা $(A^{\nu})$ নিচের নিয়ম মেনে রূপান্তরিত হয় তবে তারা একটি ফোর ভেক্টর প্রকাশ করে (আইনস্টাইনের সামেশন রীতি মাথায় রেখে),

$\displaystyle A'^{\mu} = \frac{\partial x'^{\mu}}{\partial x^{\nu}}A^{\nu} = {Lambda}^{\mu}_{\nu}A^{\nu} text{with } \mu, \nu = 0,1,2,3$ …………….(1)

যেখানে যথরীতি $\displaystyle {Lambda}^{\mu}_{\nu}=\frac{\partial x'^{\mu}}{\partial x^{\nu}}$ হল $O(x^0,x^1,x^2,x^3)$ ইনার্শিয়াল ফ্রেম থেকে $O'(x'^0,x'^1,x'^2,x'^3)$ ইনার্শিয়াল ফ্রেমে লোরেন্‍ৎস রূপান্তরণ মেট্রিক্সের $\mu$ তম সারি ও $\nu$ তম স্তম্ভের উপাদান। একইভাবে $O'(x'^0,x'^1,x'^2,x'^3)$ ফ্রেম থেকে $O(x^0,x^1,x^2,x^3)$ ফ্রেমে লোরেন্‍ৎস রূপান্তরণের ফলে,

$\displaystyle A^{\nu} = \frac{\partial x^{\nu}}{\partial x'^{\mu}}A^{\nu} = {Lambda}^{\nu}_{\mu}A'^{\mu}$

যেখানে আগের মতই $\displaystyle {Lambda}^{\nu}_{\mu}=\frac{\partial x^{\nu}}{\partial x'^{\mu}}$ হল $O'(x'^0,x'^1,x'^2,x'^3)$ ইনার্শিয়াল ফ্রেম থেকে $O(x^0,x^1,x^2,x^3)$ ইনার্শিয়াল ফ্রেমে লোরেন্‍ৎস রূপান্তরণ মেট্রিক্সের $\nu$ তম সারি ও $\mu$ তম স্তম্ভের উপাদান।

ত্রিমাত্রিক স্থানে নিউটনের গতিসূত্র লেখার সময় কণার গতিবেগ লেখা হয় নিচে দেওয়া তিনটি উপাদানযুক্ত বা ত্রিমাত্রিক ভেক্টরের মাধ্যমে,

$\displaystyle {\bf v}=\frac{d{\bf r}}{dt} implies v^i = \frac{dx^i}{dt}, i=1, 2, 3$

যেখানে ${\bf r} equiv (x^1,x^2,x^3) equiv (x,y,z)$ হল কোন ইনার্শিয়াল রেফারেন্স ফ্রেমের সাপেক্ষে কোন সময় $t$ তে ওই কণার অবস্থান। এটা দেখে মনে হতে পারে ত্রিমাত্রিক গতিবেগ ভেক্টরের সাথে আরেকটি উপাদান $\displaystyle \frac{dx^0}{dt}$ জুড়ে দিলেই তো গতিবেগের ফোর ভেক্টর তৈরি হয়ে যায়। অর্থাৎ $\displaystyle V^{\mu} = \frac{dx^{\mu}}{dt}$ -ই তো গতিবেগের ফোর ভেক্টর হতে পারে, (যেখানে $\mu =0, 1, 2, 3$ )। সত্যিই কি তাই? চল পরীক্ষা করে দেখা যাক। তার জন্যে দেখতে হবে লোরেন্‍ৎস রূপান্তরণের ফলে কিভাবে এই উপাদানগুলি পরিবর্তিত হয় (যেখানেই একই সূচকের পূনরাবৃত্তি হয়েছে সেখানেই সামেশন রীতির কথা মনে রাখবে),

$\displaystyle V'^{\mu} = \frac{dx'^{\mu}}{dt'} = \frac{dx'^{\mu}}{dx^{\nu}}\frac{dx^{\nu}}{dt}\frac{dt}{dt'} = {Lambda}^{\mu}_{\nu} V^{\nu}\frac{dt}{dt'}$ ….. (2)

যেহেতু $\displaystyle \frac{dt}{dt'} neq 1$ , তাই $V^{\mu}$ লোরেন্‍ৎস রূপান্তরণের ফলে ফোর ভেক্টর পরিবর্তনের সূত্র মেনে চলছে না। অতএব এটা গতিবেগের ফোর ভেক্টর হতে পারেনা। তাহলে উপায়? উপায় খুঁজতে হলে আমাদের মিনকোভস্কি স্থানে ইন্টারভাল ও প্রপার টাইম বা সঠিক সময়ের কথা মনে করতে হবে। তোমরা জানো যে স্পেস-টাইমে পরষ্পরের কাছাকাছি অবস্থিত দুটি বিন্দু $(ct + cdt, x+dx, y+dy,z+dz)$ এবং $(ct,x,y,z)$ -এর মধ্যে যদি স্পেস-টাইম ইন্টারভাল $ds$ হয় তবে,

$\displaystyle ds^2 = c^2dt^2 -(dx^2 + dy^2 +dz^2)$

$\displaystyle = c^2 dt^2 \left(1 - \frac{1}{c^2}\frac{dx^2+dy^2+dz^2}{dt^2}\right)$

$\displaystyle = c^2 dt^2 \left(1 - \frac{v^2}{c^2}\right)$

অর্থাৎ কোন গতিশিল কণা যদি কোন ইনার্শিয়াল ফ্রেমের সাপেক্ষে $dt$ সময়ে $P(x,y,z)$ বিন্দু থেকে $Q(x+dx, y+dy,z+dz)$ বিন্দুতে পৌঁছায় তবে তার জন্যে অতিক্রান্ত স্পেস-টাইম ইনটারভাল,

$\displaystyle ds = c dt sqrt{1 - \frac{v^2}{c^2}} = \frac{cdt}{\gamma}$

যেখানে $\gamma = 1/sqrt{1-v^2/c^2}$ । ওই মূহুর্তে $v$ বেগে চলনশীল কোন ফ্রেমের সাপেক্ষে কণাটি স্থির। সুতরাং যদি ওই ফ্রেমের ঘড়িতে কণার P থেকে Q বিন্দুতে যাওয়ার মাঝে $dtau$ সময় অতিক্রান্ত হয় তবে তোমরা জানো যে তাকে বলা হবে কণাটির প্রপার টাইম বা সঠিক সময় এবং $dtau = dt/\gamma$ । অতএব,

$\displaystyle ds = c dtau$ …………. (3)

(3) নং সমীকরণ কি করে এল সেটা আরও সহজেও বোঝা যেতে পারে। যেহেতু ইনটারভাল একটি স্কেলার তাই সমস্ত ফ্রেমের সাপেক্ষে ওর মান একই। সুতরাং যে ফ্রেমে কণাটি স্থির সেই ফ্রেমের সাপেক্ষে যদি $dtau$ সময় অতিক্রান্ত হয় তবে স্পষ্টতই $\displaystyle ds=cdtau=\frac{cdt}{\gamma}$ ।

এবারে চল দেখা যাক, $\displaystyle U^{\mu} = \frac{dx^{\mu}}{dtau}$ গতিবেগের ফোর ভেক্টর হতে পারে কিনা। সেজন্যে আমরা পরীক্ষা করে দেখব যে $U^{\mu}$ লোরেন্‍ৎস রূপান্তরণের ফলে কিভাবে পরিবর্তিত হচ্ছে?

$\displaystyle U'^{\nu} = \frac{dx'^{\nu}}{dtau} = \frac{dx'^{\nu}}{dx^{\mu}}\frac{dx^{\mu}}{dtau} = {Lambda}^{\nu}_{\mu}U^{\mu}$

অর্থাৎ $U^{\mu}$ লোরেন্‍ৎস রূপান্তরণের ফলে ফোর ভেক্টরের পরিবর্তনের সূত্র মেনে রূপান্তরিত হচ্ছে। অতএব $U^{\mu}$ গতিবেগের ফোর ভেক্টরের উপাদান হবার যোগ্য। চল এবারে দেখা যাক এই ফোর ভেক্টরের চারটি উপাদান কি কি?

$\displaystyle U^0 = \frac{dx^0}{dtau}= c\frac{dt}{dtau} = \gamma c$

$\displaystyle U^1 = \frac{dx^1}{dtau}= \gamma \frac{dx^1}{dt} = \gamma v_x$

$\displaystyle U^2 = \frac{dx^2}{dtau}= \gamma \frac{dx^2}{dt} = \gamma v_y$

$\displaystyle U^3 = \frac{dx^3}{dtau}= \gamma \frac{dx^3}{dt} = \gamma v_z$

অর্থাৎ $U^{\mu}$ ফোর ভেক্টরের সময়ের মত উপাদান (timelike component বা শূন্যতম উপাদান $U^0$ ) আলোর বেগ এবং তিনটি স্থানের মত উপাদান (space like components $U^1, U^2, U^3$ ) কণার ত্রিমাত্রিক গতিবেগ $({\bf v})$ প্রকাশ করে। সুগঠিত করে লিখলে গতিবেগের ফোর ভেক্টর ${\bf U} = \gamma (c, {\bf v})$ , যেখানে ${\bf v} = (v_x,v_y,v_z)$ । যে ফ্রেমের সাপেক্ষে কণাটির গতিবেগ শূন্য অর্থাৎ কণার সাথে একই বেগে গতিশীল ফ্রেমের সাপেক্ষে ওই কণার ফোর ভেক্টর স্বভাবতই $(c,0,0,0)$ কারণ ${\bf v} =0$ এবং $\gamma =1$ । আরও একটি বিষয় এখানে উল্লেখ করা প্রয়োজন। সেটা হল যে আলোর কোয়ান্টা ফোটনের ক্ষেত্রে গতিবেগের ফোর ভেক্টর লেখা যায়না বা সংজ্ঞা দেওয়া যায়না, কারণ ফোটনের জন্য স্পেস-টাইম ইন্টারভাল সর্বদা শূন্য, তাই $dtau =0$ । অতএব ফোর ভেক্টরের সংজ্ঞা এক্ষেত্রে প্রযোজ্য নয়। আর যদি কোন কণার বেগ আলোর বেগের থেকে অনেক কম হয় তবে গতিবেগের ফোর ভেক্টরের স্থান সম্মন্ধীয় উপাদানগুলি সাধারণ ত্রিমাত্রিক নিউটনিয় গতিবেগে পরিবর্তিত হয়, কারণ সেক্ষেত্রে $\gamma =1$ এবং ${\bf U} equiv (c,{\bf v})$ । উল্লেখযোগ্য যে ফোর ভেলোসিটিকে কখওনো কখওনো প্রপার ভেলোসিটিও বলা হয়। চল এবারে মিনকোভস্কি স্থানে গতিবেগের ফোর ভেক্টরের দৈর্ঘ্য নির্ণয় করা যাক,

$\displaystyle U_{\mu}U^{\mu} = eta_{\mu \nu}U^{\nu}U^{\mu}= \gamma^2(c^2 - v^2)=c^2$

এখানে $eta_{\mu \nu}$ হল মেট্রিক টেন্সরের উপাদানসমূহ। অর্থাৎ ভেলোসিটি ফোর ভেক্টরের দৈর্ঘ্য একটি স্কেলার রাশি যা লোরেন্‍ৎস রূপান্তরণের ফলে অপরিবর্তিত থাকে। এখানে বলে রাখছি যে কোন ফোর ভেক্টরের দৈর্ঘ্য নির্ণয়ের অর্থ হল ওই ভেক্টরের নিজের সাথেই ওর স্কেলার গুণফল বের করা। অন্যভাবে বললে ওই ভেক্টরের নিজের সাথে ওর নিজের direct গুণের (টেন্সরের আলোচনা মনে কর) ফলে যে মিশ্র টেন্সর উৎপন্ন হয় তার সংকোচন বা contraction করে ওই ফোর ভেক্টরের দৈর্ঘ্য বের করা হয়।

গতিবেগ ফোর ভেক্টরের উপরে প্রদত্ত সংজ্ঞা থেকে আশা করি তোমরা এটাও অনুমান করতে পারছ যে ত্বরণের ফোর ভেক্টর কেমন হবে। যেহেতু ত্বরণ মূলত বস্তুর গতিবেগ পরিবর্তনের হার, তাই ত্বরণের ফোর ভেক্টর $f^{\mu}$ হবে প্রপার টাইমের সাপেক্ষে কণার ফোর গতিবেগে পরিবর্তনের হার,

$\displaystyle f^{\mu} = \frac{dU^{\mu}}{dtau}$ …………… (5)

যেহেতু $dtau$ একটি স্কেলার যা লোরেন্‍ৎস রূপান্তরণের ফলে অপরিবর্তিত থাকে এবং $dU^{\mu}$ ফোর ভেক্টরের উপাদান, তাই $f^{\mu}$ একটি ফোর ভেক্টর। স্পষ্টতই ত্বরণের ফোর ভেক্টরের সময়ের মত উপাদান বা টাইম-লাইক উপাদান,

$\displaystyle f^{0} = \frac{dU^0}{dtau} = c\frac{d\gamma}{dtau}=c\frac{d\gamma}{dt}\frac{dt}{dtau}=\gamma c \frac{d\gamma}{dt} = \gamma c \frac{d}{dt}\left(1-v^2/c^2 \right)^{-1/2}$

$\displaystyle = -\frac{\gamma c}{2}\left(1-v^2/c^2 \right)^{-3/2}\left(\frac{-1}{c^2}\right)\frac{d}{dt}\left(v_x^2+v_y^2+v_z^2 \right) = \frac{\gamma^4}{2c}\left(2v_x\frac{dv_x}{dt} +2v_y\frac{dv_y}{dt} +2v_z\frac{dv_z}{dt} \right)$

বা, $\displaystyle f^{0} = \frac{\gamma^4}{c}{\bf v}.\frac{d{\bf v}}{dt} =\frac{\gamma^4}{c}{\bf v}.{\bf a}$

যেখানে $\displaystyle {\bf a}=\frac{d{\bf v}}{dt}$ হল কণার ত্রিমাত্রিক ত্বরণ।

ত্বরণ ফোর ভেক্টরের স্থানের মত (spacelike component) উপাদানগুলি,

$\displaystyle f^i = \frac{dU^i}{dtau}, i = 1, 2, 3$

বা, $\displaystyle {\bf f}= \frac{d}{dt}(\gamma {\bf v})\frac{dt}{dtau} = \gamma \frac{d}{dt}(\gamma {\bf v}) text{with } {\bf f} equiv (f^1,f^2,f^3)$

$\displaystyle = \gamma \left[ \frac{d\gamma}{dt} {\bf v} + \gamma \frac{{dbf v}}{dt} \right]$

$f^0$ বের করার পদ্ধতি অবলম্বন করে,

$\displaystyle {\bf f} = \gamma \left[\frac{\gamma^3}{c^2}({\bf v}.{\bf a}){\bf v} + \gamma {\bf a}\right] = \gamma^2 {\bf a} + \frac{\gamma^4}{c^2}({\bf v}.{\bf a}){\bf v}$

অতএব সুগঠিত করে লিখলে ত্বরণের ফোর ভেক্টর ${\bf A}$ ,

$\displaystyle {\bf A} equiv (f^0,{\bf f}) = \left(\frac{\gamma^4}{c}{\bf v}.{\bf a}, \gamma^2 {\bf a} + \frac{\gamma^4}{c^2}({\bf v}.{\bf a}){\bf v} \right)$

আবারও লিখছি যে, $\gamma = 1/sqrt{1-v^2/c^2}$ , যেখানে $v$ হল কোন মুহূর্ত $t$ -তে $O(ct,x,y,z)$ ফ্রেমের সাপেক্ষে কণাটির গতিবেগ। যদি কণাটির গতিবেগ খুব কম হয় তবে $latex v << c$ এবং $latex \gamma =1$। সুতরাং, ত্বরণের ফোর ভেক্টর $latex {\bf A} = ({\bf v.a}/c,{\bf a})$। অর্থাৎ ত্বরণ ফোর ভেক্টরের স্থান সম্মন্ধীয় উপাদানগুলি নিউটনের বলবিদ্যার সাধারণ ত্রিমাত্রিক ত্বরণে পরিণত হয়েছে। একইভাবে কণাটির সাথে কোন মুহূর্তে সমবেগে চলা ফ্রেমের সাপেক্ষে কণার ফোর ত্বরণ $latex {\bf A} = (0,{\bf a})$ কারণ এক্ষেত্রে $latex {\bf v} =0$। প্রপার সময়ের মত এই ত্বরণকে বলা হয় প্রপার ত্বরণ যা তাৎক্ষণিকভাবে কণাটির সাথে সমবেগে গতিশীল ফ্রেমের সাপেক্ষে কণার ত্বরণ মাত্র। এবারে গতিবেগ ও ত্বরণের ফোর ভেক্টরের পারষ্পারিক সম্পর্ক কেমন সেটা দেখা যাক। তোমরা জানো যে গতিবেগের ফোর ভেক্টরের দৈর্ঘ্য $latex c^2$। $latex \displaystyle U_{\mu}U^{\mu} = eta_{\mu \nu}U^{\nu}U^{\mu}=c^2$ বা, $latex \displaystyle \frac{d}{dtau}(eta_{\mu \nu}U^{\nu}U^{\mu}) = 0$ বা, $latex \displaystyle eta_{\mu \nu}\frac{dU^{\nu}}{dtau}U^{\mu} + eta_{\mu \nu}U^{\nu}\frac{dU^{\mu}}{dtau} = U_{\nu}\frac{dU^{\nu}}{dtau} + U_{\mu}\frac{dU^{\mu}}{dtau} = 2U_{\mu}\frac{dU^{\mu}}{dtau} =0$ ...... (6) কারণ $latex \displaystyle U_{\nu}\frac{dU^{\nu}}{dtau} =U_{\mu}\frac{dU^{\mu}}{dtau}$ । (6) নম্বর সমীকরণ থেকে দেখা যাচ্ছে যে গতিবেগ ও ত্বরণের ফোর ভেক্টর পরষ্পরের সাথে অর্থোগোনাল (orthogonal)। এর পরের পোস্টে আমরা এই গতিবেগ ও ত্বরণের ফোর ভেক্টর ব্যবহার করে নিউটনের গতিসূত্র লিখব ও সেখান থেকে ভর ও শক্তির তুল্যতা আলোচনা করব। 🙂

11 thoughts on “মিনকোভস্কি স্থানে গতিবেগ ও ত্বরণের ফোর ভেক্টর (Four velocity and accelaration)”

shariful islam says:

May 6, 2014 at 6:58 pm

ভাই আপনার নাম আমি জানি না। তবে আমি (শরিফ) এবং আমার বন্ধু মিঠুন আপনার খুব ভক্ত। আপনি খুব ভাল লেখেন। আমার এবং মিঠুনের দুইটা সমীকরণ জানা খুব দরকার। আমাদের মনে হয় আপনি সমীকরণদুইটি বলতে পারবেন। যদি জানেন দয়া করে জানাবেন।
1. উপবৃত্তের কেন্দ্রপ্রসারী বলের সমীকরণটি কি হবে?
2. একটা q চার্জে চার্জিত বস্তু যদি তার নিজ কেন্দ্রগামী অক্ষের সাপেক্ষে ঘূর্ণায়মান থাকে (স্পিনিং আরকি) তবে তার দ্বারা r দূরত্বে তৈরী চৌম্বক ক্ষেত্রের মানের ফরমূলা কী? ‘ক্ষেত্রের’ জায়গায় ‘ভ্রামকের’ ফরমূলা হলেও চলবে।

সবথেকে ভাল হয় ইমেই করে জানালে। sharifmd98@yahoo.com

Reply
1. admin says:
  
  May 6, 2014 at 7:51 pm
  
  ধন্যবাদ শরিফ (এবং মিঠুন)। শুনে খুব ভালো লাগল যে আমার লেখা তোমাদের ভালো লাগে। আশা করি আরও ভালো ভালো লেখা লিখতে পারব।
  
  Reply
2. admin says:
  
  May 6, 2014 at 8:09 pm
  
  চেষ্টা করব ওই দুটো প্রশ্নের উত্তর মেইল করার। তোমাদের যখন দরকার তখন তাড়াতাড়িই মেইল পেয়ে যাবে। good luck।
  
  Reply
3. admin says:
  
  May 7, 2014 at 2:11 pm
  
  @ শরিফ ও মিঠুন, আশাকরি উপবৃত্ত বলতে তোমরা উপবৃত্তাকার কক্ষপথের কথা বলছ, যা মূলত কেন্দ্রীয় বলের প্রভাবে কোন কণার গতিপথ। যদি কোন মুহূর্তে এই কক্ষপথে গতিশীল কোন m ভরবিশিষ্ট কণার অবস্থানের পোলার কোঅর্ডিনেট $(r, theta)$ হয় তবে কেন্দ্রপ্রসারী বলের (centrifugal force) মান হল $L^2/(mr^3)$ , যেখানে L হল কণার কৌণিক ভরবেগ (angular momentum), যা কেন্দ্রীয় বলের প্রভাবে গতির জন্য ধ্রুবক। মনে রাখবে যে উপবৃত্তাকার কক্ষপথের জন্য কিন্তু r সময়ের সাথে পরিবর্তিত হয় এবং কেন্দ্রীয় বলের জন্য কণার গতির সমীকরণ, $mddot{r} = frac{L^2}{mr^3} + F_c$ , যেখানে $F_c$ হল প্রযুক্ত কেন্দ্রীয় বল। মহাকর্ষের জন্য $F_c = frac{C}{r^2}$ , C হল ধ্রুবক। $L = mr^2dot{theta}$ ।
  
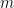  ঘূর্ণায়মান আধানের জন্য চৌম্বক ক্ষেত্রের ভ্রামকের (magnetic moment) মান হল $boldsymbol {mu} = frac{q}{2m}{bf L}$ , যেখানে $m$ হল কণার ভর ও ${bf L}$ হল কণার কৌণিক ভরবেগ (angular momentum)।
  
  Reply
মিঠুন রায় says:

May 7, 2014 at 3:08 pm

আমাদের সাহায্য করার জন্য আপনাকে অনেক ধন্যবাদ এডমিন. 🙂
আমার বিশ্বাস এই ব্লগটা বাংলায় পদার্থবিজ্ঞান চর্চার জন্য এক বিশেষ ক্ষেত্র হিসেবে গড়ে উঠবে

Reply
shariful islam says:

May 7, 2014 at 4:29 pm

ভাই আমি সমীকরনটা পদার্থবিজ্ঞানের একট সমস্যায় ব্যাবহার করতে চাই। কিন্তু কোনের মানটা কিভাবে ব্যাবহার করব তাই বুঝতে পারছি না। যেমন আমরা বৃত্তের জন্য কেন্দ্রপসারী বলের সমীকরণটা জানি, F = (m v^2)/r । এখানে r হল বৃত্তের ব্যাসার্ধ্য। উপবৃত্তের জন্য কি এমন কোন সমীকরণ আছে যেখানে কেন্দ্রপ্রসারী বল কণাটি যে নাভিকে কেন্দ্রকরে ঘুরছে সেই নাভি থেকে দূরত্বের সাথে সম্পর্কিত? আসলে আমি বলতে চাচ্ছি একটি কণা যদি উপবৃত্তাকার পথে ঘোরে তাহলে তার এই কক্ষপথের কেন্দ্রপ্রসারী বলের সমীকরণ কত হবে?
আপনাকে বারবার বিরক্ত করার জন্য আমি দু:খিত। হয়তো আমার কথাগুলো আমি আপনাকে প্রথমে বুঝাতে পারি নি। কিন্তু আমার মানটি খুব প্রয়োজন বলেই বারবার আপনাকে বিরক্ত করছি। দয়াকরে কিছু মনে করবেন না।

Reply
1. admin says:
  
  May 7, 2014 at 8:01 pm
  
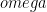  কেন্দ্রপ্রসারী বলের সমীকরণটা আমি লিখেই দিয়েছি এর আগের পোস্টে। ওখানে $(r,theta)$ হল উপবৃত্তের কেন্দ্রের সাপেক্ষে বস্তুর কোন মুহূর্তে অবস্থান। অর্থাৎ উপবৃত্তের কেন্দ্র থেকে বস্তুটির দূরত্ব হল $r$ এবং এই ${bf r}$ ভেক্টর $x$ -অক্ষের সাথে যে কোন তৈরি করে তাই হল $theta$ । আরও পরিষ্কার করে বললে $x = r text{cos}theta, y = rtext{sin}theta$ । আর $dot{theta}$ হল বস্তুটির কৌণিক গতিবেগ $omega$ যা বস্তুটির কোন মুহূর্তের রৈখিক গতিবেগের সাথে এইভাবে সম্পর্কযুক্ত $omega = vr$ । সুতরাং দেখতে গেলে উপবৃত্তাকার কক্ষপথের জন্যেও কোন মুহূর্তে কেন্দ্রপ্রসারী বলের মান $L^2/mr^3 = mv^2/r$ , শুধু বৃত্তাকার পথের সাথে পার্থক্য এই যে বৃত্তের জন্যে $v$ এবং $r$ ধ্রুবক, কিন্তু উপবৃত্তের জন্যে ওগুলো সময়ের সাথে পরিবর্তনশীল। তুমি ঠিক কোন সমস্যায় এই সমীকরণ ব্যবহার করতে চাও সেটা জানালে আরও ভালভাবে সাহায্য করতে পারি। 🙂
  
  Reply
মিঠুন রায় says:

May 7, 2014 at 5:20 pm

ঘূর্ণায়মান চার্জের সমস্যাটায় ‘চৌম্বক ক্ষেত্র’ বের করার ফরমূলাটা বলা যাবে কি? উপকার হত 🙂

Reply
1. admin says:
  
  May 8, 2014 at 2:23 pm
  
  অনেক ধন্যবাদ মিঠুন। ${boldsymbol {mu}}$ মোমেন্ট বা ভ্রামকবিশিষ্ট ডাইপোলের জন্য r দূরত্বে চৌম্বক ক্ষেত্র $displaystyle {bf B} = frac{mu_0}{4pi}left[frac{3{bf r}(boldsymbol {mu}.{bf r})}{r^5} - frac{boldsymbol {mu}}{r^3}right]$ । এখানে $mu_0$ হল শূন্যস্থানের চৌম্বক ভেদ্যতা।
  
  Reply
shariful islam says:

May 8, 2014 at 7:41 am

আপনাকে অসংখ্য ধন্যবাদ। আমি বুঝতে পেরেছি।
আপনার ব্লগে একটা প্রশ্ন-উওর অংশ থাকলে মনে হয় ভাল হতো। যাই হোক শুভ কামনা রইল…

Reply
1. admin says:
  
  May 8, 2014 at 2:16 pm
  
  🙂 একটা প্রশ্নোত্তর বিভাগ খোলার চেষ্টা করছি। আশাকরি তাড়াতাড়িই সেটা সম্ভব হবে। ধন্যবাদ শরিফ।
  
  Reply