এক্সপেকটেশন ভ্যালূ গণনা – একটি উদাহরণ

আজ আমাদের আলোচ্য বিষয় হল কোন একটি প্রদত্ত ওয়েভ ফাংশন থেকে বিভিন্ন পরিমাপযোগ্য রাশির এক্সপেকটেশন ভ্যালূ গণনা। এর আগের পোস্টের প্রবন্ধটি পড়ে থাকলে আজকের এই বিষয়টি বুঝতে তোমাদের বিন্দুমাত্র অসুবিধা হবেনা; উল্টে তোমরাই আমাকে শিখিয়ে দিতে পারবে! তবুও সম্পূর্ণতার স্বার্থে আমি একটি উদাহরণ দিয়ে ব্যাপারটি একটু আলোচনা করব। ধর আমরা কোন একটি কোয়ান্টাম কণার গতি সম্পর্কিত বিভিন্ন পরিমাপযোগ্য রাশি যেমন অবস্থান ( $x$ ), ভরবেগ ( $p$ ) এবং গতিশক্তির ( $E_k$ ) এক্সপেকটেশন ভ্যালূ বা গড় মান নির্ণয় করতে চাই। সেজন্য আমাদের প্রথমেই যেটা চাই সেটা হল ওই কণার ওয়েভ ফাংশন। ওয়েভ ফাংশন কিভাবে গণনা করতে হয় সেটা তোমরা এর পরের পোষ্টে দেখতে পাবে। আজ আমি একটি ওয়েভ ফাংশন তোমাদের দিয়ে দেব! এখানে এটা বলে রাখি যে আজকের এই আলোচনা খুব বেশি করে ক্যালকুলাস নির্ভর। যারা ক্যালকুলাস জানেনা তাদের অনুরোধ করছি দয়া করে ক্যলকুলাস শিখে নিতে, নাহলে কোয়ান্টাম মেকানিক্স বুঝতে অসুবিধা হবে।

প্রদত্ত ওয়েভ ফাংশনঃ

$\displaystyle Psi(x) =\left{ begin{matrix} sqrt{\frac{2}{L}} text{sin}(pi\frac{x}{L}) & text{ if } 0<x<L \ 0 & text{ if } x \leq 0 text{ and } x \geq L end{matrix} \right.$

অর্থাৎ $x$ এর মান 0 থেকে $L$ -এর মাঝে থাকলে তবেই ওয়েভ ফাংশনের মান শূন্য নয় (non zero)। $x$ এর অন্য সব মানের জন্য ওয়েভ ফাংশনের মান শূন্য (zero)। (আমরা আজকের আলোচনার জন্য ওয়েভ ফাংশনের সময়ের উপর নির্ভরতা বিষয়টিকে উপেক্ষা করব।) একটি বিশেষ সিষ্টেমের ক্ষেত্রে এরকম ওয়েভ ফাংশন সম্ভব। সেটা হল ইনফাইনাইট কোয়ান্টাম ওয়েল (infinite potential well)। প্রথমেই আমাদের দেখে নিতে হবে যে ওয়েভ ফাংশনটি নর্মালাইজ করা আছে কিনা? যদি তা না থাকে তবে নর্মালাইজ করে নিতে হবে।

$\displaystyle \int_{-infty}^{infty} |Psi(x)|^2 mathrm{d}x=\int_0^L |Psi(x)|^2 mathrm{d}x = \int_0^L Psi(x)^*. Psi(x) mathrm{d}x$

এখানে যেহেতু ওয়েভ ফাংশনটি জটিল রাশি নয়, তাই $Psi(x) = Psi(x)^*$ । অতএব,

$\displaystyle \int_{-infty}^{infty} |Psi(x)|^2 mathrm{d}x = \int_0^L Psi(x)^2 mathrm{d}x = \frac{2}{L}\int_0^Lmathrm{sin}^2 \left(pi\frac{x}{L}\right) mathrm{d}x$

$\displaystyle= \frac{1}{L}\int_0^L\left[1-mathrm{cos} \left(2pi\frac{x}{L}\right)\right] mathrm{d}x$

$\displaystyle=1-\frac{1}{L}\int_0^Lmathrm{cos} \left(2pi\frac{x}{L}\right) mathrm{d}x = 1 - 0 = 1$

অর্থাৎ ওয়েভ ফাংশনটি নর্মালাইজ করা আছে। চল এবারে অবস্থানের এক্সপেকটেশন ভ্যালূ বা গড় নির্ণয় করা যাক। নিশ্চয়ই তোমাদের মনে আছে যে অবস্থানের অপারেটর হল $x$ । আর,

$\displaystyle \langle x\rangle = \int_0^L Psi(x). x . Psi(x) mathrm{d}x = \int_0^L x.Psi(x)^2 mathrm{d}x$

$\displaystyle = \frac{2}{L}\int_0^Lx.mathrm{sin}^2 \left(pi\frac{x}{L}\right) mathrm{d}x = \frac{L}{2}$ [এই ইন্টিগ্রেশনটিকে ইন্টিগ্রেশন বাই পার্টস নিয়ম প্রয়োগ করে সহজেই করা যায়।]

সুতরাং অবস্থানের গড় $L/2$ । চল এবারে $\langle x^2\rangle$ -এর মান বের করা যাক।

$\displaystyle \langle x^2\rangle = \frac{2}{L}\int_0^Lx^2 mathrm{sin}^2 \left(pi\frac{x}{L}\right) mathrm{d}x = \frac{L^2}{3}-\frac{L^2}{2pi^2}$ [এই ইন্টিগ্রেশনটিকেও “ইন্টিগ্রেশন বাই পার্টস” নিয়ম মেনে করা হয়েছে। নিজেরা পরীক্ষা করে দেখ ঠিক আছে কিনা।]

অবস্থানের আনসার্টেনটি,

$\displaystyle \Delta x = sqrt{\langle x^2\rangle - \langle x \rangle^2} = sqrt{\frac{L^2}{3}-\frac{L^2}{2pi^2} - (\frac{L}{2})^2}$

$\displaystyle= \frac{L}{2pi}sqrt{(pi^2-6)/3} approx \frac{L}{2pi}$

একইরকম ভাবে ভরবেগের এক্সপেকটেশন ভ্যালূ বা গড় মান,

$\displaystyle \langle p\rangle = \int_0^L Psi(x)^*.hat{p}. Psi(x) mathrm{d}x = \frac{2}{L}\int_0^L mathrm{sin} \left(pi\frac{x}{L}\right)^* \left(-i\hbar\frac{\partial}{\partial x}\right) mathrm{sin} \left(pi\frac{x}{L}\right) mathrm{d}x$

$\displaystyle = -i\hbar\frac{2pi}{L^2}\int_0^L text{sin} \left(pi \frac{x}{L} \right) text{cos} \left( pi \frac{x}{L}\right) text{d} x$

$\displaystyle = -i\hbar\frac{pi}{L^2}\int_0^L text{sin} \left( 2pi\frac{x}{L}\right) text{d} x = 0$

$p^2$ -এর এক্সপেকটেশন ভ্যালূ,

$\displaystyle \langle p^2 \rangle = \int_0^L Psi(x)^* . hat{p}^2 . Psi(x)mathrm{d}x$

$\displaystyle = \frac{2}{L}\int_0^L mathrm{sin} \left(pi\frac{x}{L}\right)^* \left(-i\hbar\frac{\partial}{\partial x}\right)^2 mathrm{sin} \left(pi\frac{x}{L}\right) mathrm{d}x$

$\displaystyle= -\frac{2\hbar^2}{L}\int_0^L mathrm{sin} \left(pi\frac{x}{L}\right).\frac{\partial^2}{\partial x^2} mathrm{sin} \left(pi\frac{x}{L}\right) mathrm{d}x = -\frac{2{\hbar}^2{pi}^2}{L^3}\int_0^L mathrm{sin} \left(pi\frac{x}{L}\right) mathrm{sin}\left(pi\frac{x}{L}\right) mathrm{d}x$

$\displaystyle= -({pi}^2{\hbar}^2/L^3)\int_0^L \left[1-mathrm{cos} \left(2pi\frac{x}{L}\right)\right] mathrm{d}x$

$\displaystyle= -({pi}^2{\hbar}^2/L^3).(L -0) = (pi^2\hbar^2/L^2)$

অতএব ভরবেগের আনসার্টেনটি,

$\displaystyle \Delta p = sqrt{\langle p^2 \rangle -\langle p \rangle^2} = \frac{pi\hbar}{L}$

তাহলে দেখতে পাচ্ছ যে,

$\displaystyle \Delta x . \Delta p = \frac{L}{2pi}. \frac{pi\hbar}{L} = \frac{\hbar}{2}$

বলার অপেক্ষা থাকেনা যে এটাই আনসার্টেনটি নীতি। আমাদের পরবর্তী গন্তব্য গতিশক্তির গড় মান। আগেই দেখেছো যে $E_k = p^2/2m$ । সুতরাং গতিশক্তির গড় বা এক্সপেকটেশন ভ্যালূ,

$\displaystyle \langle E_k \rangle = \langle p^2 \rangle / 2m = \frac{pi^2 \hbar^2}{2m L^2}$ .

দেখলে তো, কোন ওয়েভ ফাংশন দেওয়া থাকলে বিভিন্ন পরিমাপযোগ্য রাশির এক্সপেকটেশন ভ্যালূ বের করা কত সহজ! আসল সমস্যাটা হয় ওয়েভ ফাংশন বের করাতেই। যাইহোক আজ এই পর্যন্তই রইল। আবার শীঘ্রই দেখা হবে।

6 thoughts on “এক্সপেকটেশন ভ্যালূ গণনা – একটি উদাহরণ”

মিঠুন রায় says:

May 28, 2014 at 4:48 pm

যথেস্থ সহজ এবং মজারও বটে 🙂
মাঝখনে একজায়গায় ওটা কি অনিশ্চয়তার নীতির গাণিতিক প্রমান ছিল ? মানে, ওটাকে কি অন্যতম প্রমান হিসেবে গণ্য করা যাবে?

1. admin says:
  
  May 28, 2014 at 11:11 pm
  
  ওটা কেবল অসীম কোয়ান্টাম ওয়েলের গ্রাউন্ড স্টেটের ক্ষেত্রে প্রযোজ্য অনিশ্চয়তা নীতির প্রমান, সাধারণ প্রমান নয়। কোয়ান্টাম মেকানিক্সের ফর্মালিজম সম্মন্ধে আলোচনার সময় অনিশ্চয়তা নীতির সাধারণ (general) প্রমাণ দিয়ে দেব। 🙂 আশা করছি তাড়াতাড়ি দিতে পারব প্রমাণ টা।
  
shariful islam says:

August 26, 2014 at 5:31 pm

ইন্টিগ্রেশন বাই পার্টস নিয়মটা সংক্ষেপে একটু আলোচনা করলে উপকার হয়। বেশ কয়েকটা গাণিতিক সমাধান ভালভাবে বুঝতে পারিনি।

1. admin says:
  
  September 1, 2014 at 12:36 pm
  
  ইন্টিগ্রেশন বাই পার্টস হল ইন্টিগ্রেশন করার একটি নিয়ম। ধর দুটি ফাংশন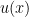 $u(x)$ এবং $v(x)$ । তবে তাদের গুণফলের ইন্টিগ্রেশন,
  $displaystyle int u(x)v(x) dx = u(x)int v(x) dx + int frac{du}{dx} left[int v(x) dxright] dx$
  
  এটাই ইন্টিগ্রেশন বাই পার্টসের নিয়ম।
  
shariful islam says:

August 26, 2014 at 5:38 pm

আরেকটা কথা। ভরবেগের গড় মানের 2য় লাইনে 2/L এর সাথে গুন হিসাবে pi/L কিভাবে আসল বুঝতে পারিনি।

1. admin says:
  
  August 26, 2014 at 6:51 pm
  
  $text{sin}(pi x/L)$ কে $x$ এর সাপেক্ষে ডিফারেনশিয়েট করার ফলেই ওটা এসেছে।